Координатами называются угловые и линейные величины (числа), определяющие положение точки на какой-либо поверхности или в пространстве.
В топографии применяют, такие системы координат, которые позволяют наиболее просто и однозначно определять положение точек земной поверхности как по результатам непосредственных измерений на местности, так и с помощью карт. К числу таких систем относятся географические, плоские прямоугольные, полярные и биполярные координаты.
Географические координаты (рис.1) – угловые величины: широта (j) и долгота (L), определяющие положение объекта на земной поверхности относительно начала координат – точки пересечения начального (Гринвичского) меридиана с экватором. На карте географическая сетка обозначена шкалой на всех сторонах рамки карты. Западная и восточная стороны рамки являются меридианами, а северная и южная – параллелями. В углах листа карты подписаны географические координаты точек пересечения сторон рамки.
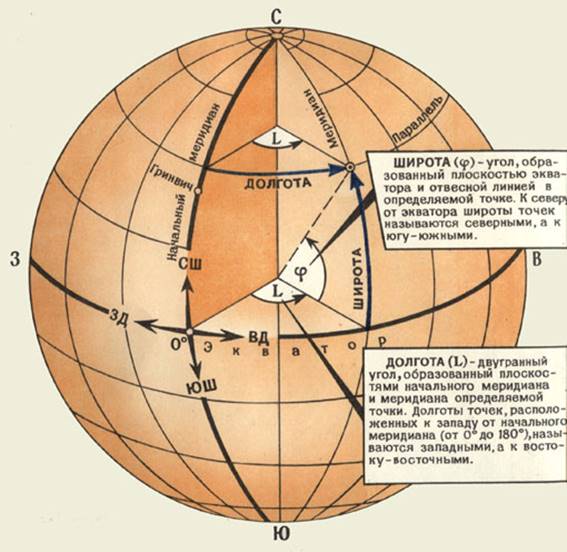
В системе географических координат положение любой точки земной поверхности относительно начала координат определяется в угловой мере. За начало у нас и в большинстве других государств принята точка пересечения начального (Гринвичского) меридиана с экватором. Являясь, таким образом, единой для всей нашей планеты, система географических координат удобна для решения задач по определению взаимного положения объектов, расположенных на значительных расстояниях друг от друга. Поэтому в военном деле эту систему используют главным образом для ведения расчетов, связанных с применением боевых средств дальнего действия, например баллистических ракет, авиации и др.
Плоские прямоугольные координаты (рис. 2) – линейные величины, определяющие положение объекта на плоскости относительно принятого начала координат – пересечение двух взаимно перпендикулярных прямых (координатных осей Х и Y).
В топографии каждая 6-градусная зона имеет свою систему прямоугольных координат. Ось Х — осевой меридиан зоны, ось Y – экватор, а точка пересечения осевого меридиана с экватором – начало координат.
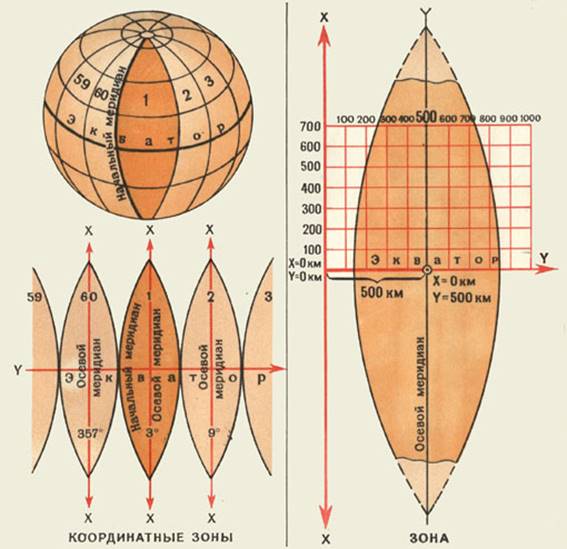
Система плоских прямоугольных координат является зональной; она установлена для каждой шестиградусной зоны, на которые делится поверхность Земли при изображении ее ни картах в проекции Гаусса, и предназначена для указания положения изображений точек земной поверхности на плоскости (карте) в этой проекции.
Началом координат в зоне является точка пересечения осевого меридиана с экватором, относительно которой и определяется в линейной мере положение всех остальных точек зоны. Начало координат зоны и ее координатные оси занимают строго определенное положение на земной поверхности. Поэтому система плоских прямоугольных координат каждой зоны связана как с системами координат всех остальных зон, так и с системой географических координат.
Применение линейных величин для определения положения точек делает систему плоских прямоугольных координат весьма удобной для ведения расчетов как при работе на местности, так и на карте. Поэтому в войсках эта система находит наиболее широкое применение. Прямоугольными координатами указывают положение точек местности, своих боевых порядков и целей, с их помощью определяют взаимное положение объектов в пределах одной координатной зоны или на смежных участках двух зон.
Системы полярных и биполярных координат являются местными системами. В войсковой практике они применяются для определения положения одних точек относительно других на сравнительно небольших участках местности, например при целеуказании, засечке ориентиров и целей, составлении схем местности и др. Эти системы могут быть связаны с системами прямоугольных и географических координат.
Читать полный конспект Определение координат точек местности (объектов)